这是 SICP 第一章的内容总结,包含了所有习题的答案。过程抽象是编程最重要的特性之一,本文阐释了为什么要进行过程抽象,如何进行好过程抽象,过程抽象的主要实践,对不同过程抽象的时间和空间认识,如何进行抽象的抽象,如何基于抽象的抽象进行工作,以及在什么时候需要什么层次的抽象这几个问题。
程序设计基本元素
John Locke 在 1690 年《有关人类理解的随笔》中写到:心智的活动,除了产生各种简单的认识外,还通过组合的方式形成复合认识,此外还可以将两个简单或复合认识对照以获得相对关系,将有关认识和所有其它认识隔离开,就是抽象,所有具有普遍性的认识都是这样得到的。
计算过程是一种抽象,它对数据进行操控(简单理解为,数据是我们希望操作的东西,而过程则是对这些数据操作的规则的描述)。我们通过一种叫做程序的规则模式来指导计算过程的进行,程序需要极其精确,一丁点的错误就会导致复杂而无法预料的后果。软件工程师通过组织自己的程序,并且预估且确信程序产生的计算过程能够完成预期的工作。
为了进行编程,使用 John McCarthy 设计的 LISt Processing 表处理 - LISP 语言,这是一种数学记述形式,最初被用来提供符号计算,而对于数值计算效率较低,但随着 Lisp 编译器编译为机器码,LISP 成为了一种实用的程序设计语言,也是继 Fortran 以来今天广泛使用的第二历史悠久的语言。LISP 有非常鲜明的特点:计算过程本身可被表示为 Lisp 数据,而在几乎所有其它语言中,都依赖主动的过程和被动的数据之间的划分,因为 Lisp 数据即过程的特点,或者将过程表示为数据的能力,使得 Lisp 成为此种用途最方便的语言,比如解释器、编译器等。
根据洛克关于认识的观点,程序设计的基本元素很容易归纳为:①基本表达形式;②组合的方法;③抽象的方法。每种强大的编程语言都提供这三种机制。
对于 Lisp 而言,最基本的表达式就是数,而组合的方法就是通过 ( op param1 param2 ..) 的复合表达式来进行表述,也称之为组合式,( ) 这样的记号称之为表,表中空格分隔的叫做元素,最左边的元素为运算符,其余元素为运算对象。 相比较其余编程语言,Lisp 这种组合的形式称之为前缀表示,其主要优点在于可传入任意实参而不会具有歧义:(+ 1 2 3 4 5),且可直接扩充允许组合式嵌套,即组合式的元素本身可以是组合式,比如:
(+ (* 3
(+ (* 2 4)
(+ 3 5)
(+ (- 10 7)
6))
注意,组合式的元素,包含运算对象和运算符,函数的参数是另一个函数在别的语言很常见:add(1,sub(3,1)),但函数本身通过函数得到在别的语言中通常写法很丑陋,比如:call(1 > 2 ? sum : sub, 1, 2),这里主要的限制在于拐了个弯,通过另一个函数来进行第一个参数作为运算符,其余作为运算对象的调用 —— 看起来就好像是对前缀表示的拙劣模仿:((if (> 1 2) + -) 1 2 3 4 5) 这种形式纯粹又干练的表达了相同的含义。
下图展示了一般过程中 LISP 程序/数据的组成部分:
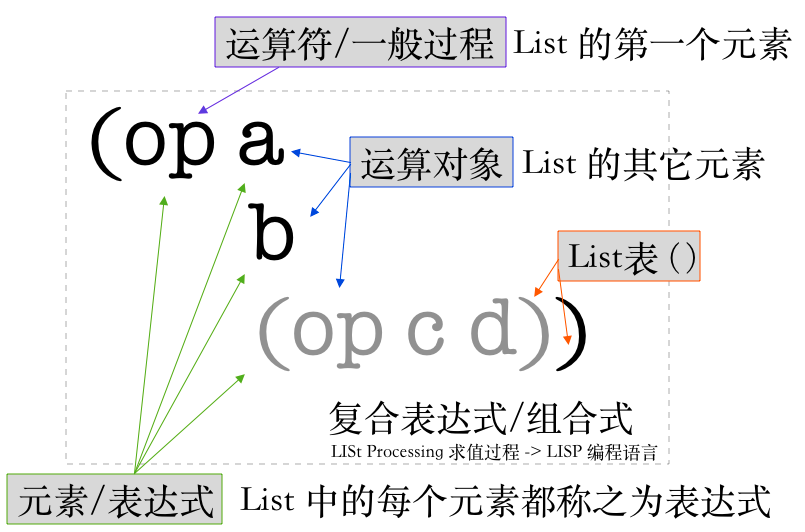
上述复合表达式组合的过程称之为一般过程,此外 Scheme 还有几种特殊过程,特殊过程具有区别一般过程的求值方式:一般过程的运算符都是机器指令,其表达式求值过程就是将多个运算对象根据指令进行数学和逻辑运算的过程 —— 这和实际计算机的实现原理一致,而特殊过程的特殊之处就在于具有特殊的内置的求值过程(特殊形式就是所谓的语言的抽象,想象洛克的话)。一般过程 + 所有的特殊过程,合起来就是 Lisp 所有的语法。对于 Scheme 这种 Lisp 方言而言,一种最基础的特殊过程就是定义 define,其写法如下:(define label value),之后在某个上下文(默认是全局环境)下 label 这个名字标识符就被关联到这个 value 对象上了,可随意使用。
对于复合表达式(组合式)的求值过程,Lisp 做的很简单,其简单的①对此组合式的每个子表达式求值,②将作为最左子表达式(运算符)的过程应用于相应的实际参数,即其它子表达式(运算对象)的值。在实际计算中,①数的值就是它们表示的数值,②内部运算符的值就是机器指令序列,③其它名字值就是环境中关联的这一名字的那个对象(内部运算符可以看做一个特殊的全局环境中的名字,指令序列就是与之关联的值)。之所以说 LISP 的数据即过程,原因是上述一般过程的定义中,其可以直接表示为一个树,就像传统语言中的数据结构:List(op, a, b, List(op c d)) 一样,这种特殊性意味着 LISP 不需要前端编译器,过程本身就是解释器需要的数据,而不用像其他语言一样要先进行语法和词法分析,然后将代码转换为 AST 树。
跟着洛克的思想,我们定义了基本认识:数,定义了数的组合方式:列表、运算符、运算对象、复合表达式,定义了一种抽象:定义 define。定义的求值过程和一般过程完全不同,可以看做是解释器自行在内部实现的。而为了提高程序语义,有必要进一步抽象,这就是过程定义,过程定义抽象了过程本身,其写法如下 (define (
(define (square x) (* x x))
(define (sum-of-square x y) (+ (square x) (square y)))
(define (f a) (sum-of-square (+ a 1) (* a 2)))
过程(一般过程和复合过程)应用的代换模型很容易表述,不过有两种实现,其一是正则序,即惰性求值,这种方式先代换,后计算,比如上述的 (f 5),先通过过程定义提取出 f:(sum-of-square (+ 5 1) (* 5 2)),依次递归提取 sum-of-squre:(+ (square (+5 1) (square (* 5 2))),再提取 square:(+ ((* (+5 1) (+5 1)) (* (* 5 2) (* 5 2)))) 最后得到 136。其二是应用序,这种方式边代换边计算,比如上述的 (f 5),先代换为 (sum-of-square (+ 5 1) (* 5 2)) 后,立刻计算运算对象,得到 (sum-of-square 6 10),之后继续代换,得到 (+ (square 6) (square 10)),这里无法计算,再次代换:(+ (* 6 6) (* 10 10)),最后得到 136。需要注意,实际解释器并非按照代换的方式直接操作过程正文,而是用值代换形参来求值,一般通过提供形参的局部环境的方式实现代换效果。Lisp 采用应用序求值,因为这样可以避免对表达式重复求值的情况,可提高效率。
下面这个例子展示了基于欧几里得算法的最大公约数的复合过程,对于 (gcd 206 40) 应用序只需要 5 次,而正则序在这 5 个节点下,每一个都包含了数个分支,导致重复计算极其严重。概括来说,正则序的低效,主要表现在重复计算,而重复计算则多出现在“递归或迭代中函数的结果要作为函数的参数在下一轮使用”的情况。
(define (gcd a b) (if (= b 0) a (gcd b (remainder a b))))
应用序:
(gcd 206 40)
(gcd 40 (R 206 40))
(gcd 6 (R 40 6))
(gcd 4 (R 6 4))
(gcd 2 (R 2 2))
正则序:
(gcd 206 40)
(gcd 40 (R 206 40))
(gcd (R 206 40) (R 40 (R 206 40)))
(gcd (R 40 (R 206 40)) (R (R 206 40) (R 40 (R 206 40))))
(gcd (R (R 206 40) (R 40 (R 206 40))) (R (R 40 (R 206 40)) (R (R 206 40) (R 40 (R 206 40))))
这里将再介绍两种特殊形式,用于执行分情况分析,一种是 cond,一种是 if,其写法分别如下所示:(cond (<p1> <e1>) (<p2> <e2>) (else <e3>)) 和 (if (<p1>) <e1> <e2>)。注意,cond 每一个谓词和表达式都放在一个 List 中,if 的谓词单独放在一个 List 中,条件则和谓词的值并列作为 if 的运算对象。Scheme 除了 > < 和 =,还提供了三种内置的逻辑复合运算符,比如:(and <e1> .. <en>) (or <e1> .. <en>) (not <e>)。因此可定义:
(define (>= x y) (not (< x y))
(define hour 13)
(define say-hello (if (> hour 11) "morning" "noon"))
(define to-do (cond ((and (> hour 6) (< hour 18)) "work") (else "sleep"))
注意,特殊形式的 cond 和 if 并不是完全类似的,因为 Scheme 实际使用应用序的问题,因此如左图所示代码,cond 无法替代 if —— 在简单情况下可以,但如果传入的分支为无限循环,应用序将导致直接卡死,这和实际 if 过程不一致。
;应用序问题
(define (if-2 pre-c then-c else-c)
(cond (pre-c then-c) (else else-c)))
(display "\n")
(display (if-2 (> 2 1) 10 20))
计算之所以提供了“怎么做”而非数学上“是什么”的框架,左边求平方根的代码就能很好的说明。数学上,平方根的描述就是值的平方等于原来的值,这并没有为怎么做提供指导。
;是什么和怎么做的区别,一个实现求平方的复合过程
(define (sqrt-original x g)
(if (< (/ (if (< (- x (* g g)) 0)
(- (- x (* g g)))
(- x (* g g)))
x)
0.01)
g
(sqrt-original
x (/ (+ (/ x g) g) 2))))
定义过程,以及将大过程分解为小部分过程:即过程抽象。过程抽象是一个黑盒,其隐藏了一些细节,其他程序员无需知道如何实现就可以使用。过程抽象的最大特征就是形式参数灵活的绑定变量(注意区分外部符号的自由变量),其虽然明显,但意义深远,比如这里基于绑定变量实现的迭代/递归。基于一般复合过程(上图)是无法实现 sqrt 这样的过程的,因为这里的 g 无法传入。过程抽象的用途在于三点:①过程隔离:将过程进行划分,使得结构更清晰,但这并不是主要目的,且要不要将一段步骤放入黑盒是一件需要慎重抉择的事情。②值的重用:过程抽象可避免对同一过程计算多次,需配合定义 define 使用。更重要的,得益于绑定变量,可以基于抽象了的过程片段实现众多类似抽象,实现了③代码复用,增强了语言表述过程的能力。但也要注意,模板,即抽象出什么参数,返回什么值,抽象过程的边界在哪里都需要仔细设计,以求最大限度的复用代码:Lisp 相比较 Fortain 最大的不同在于,前者的过程抽象少,但复用程度高,后者的过程抽象多,但复用程度低,基本是为了划分过程而进行的抽象。基于过程抽象实现的递归/迭代,比如 guess-sqrt 和 imporove-sqrt 则将描述复杂过程的代码复用能力发挥的淋漓尽致。
;过程抽象的内涵:捕获变量(形参)和自由变量(外部符号)
(display "\nFor Sqrt: \n")
(define (abs x) (if (< x 0) (- x) x))
(define (is-good-sqrt-1)
(< (abs (- x (* g g))) 0.01))
(define (is-good-sqrt-2 x g)
(< (/ (abs (- x (* g g))) x) 0.01))
(define (improve-sqrt x g)
(guess-sqrt x (/ (+ (/ x g) g) 2)))
(define (guess-sqrt x g)
(if (is-good-sqrt-2 x g) g
(improve-sqrt x g)))
(define (sqrt x) (guess-sqrt x 1.0))
(display (sqrt 10))
虽然过程抽象隐藏了细节,但对大型程序,这样的过程名也是不必要的干扰,可以将过程定义进行嵌套,这称之为块结构,这可以更有效的隐藏实现的细节。在 Java 等语言中不具备函数嵌套函数的能力,但 Java 有 OOP 和修饰符控制可见性。过程抽象主要目的是代码复用,非块结构的过程抽象一般为了其他过程复用,块结构的过程抽象一般是为了自行复用:一般用于利用形参可变进行递归。因此,如果过程抽象仅涉及自身,那么使用块结构是一种良好的工程实践。
;块结构:嵌套的定义,更清晰的结构
(printf "\nFor Cube: \n")
(define (cube x)
(define (is-good-cube x g)
(< (/ (abs (- x (* g g g))) x) 0.01))
(define (improve-cube x g)
(guess-cube x (/ (+ (/ x (* g g))
(* g 2)) 3)))
(define (guess-cube x g)
(if (is-good-cube x g) g
(improve-cube x g)))
(guess-cube x 1.0))
(display (cube 10))
下面是等价的 Scala 块结构实现,可以看到,这里的思想是类似的,唯一的区别就是动静类型以及前缀表达式(前缀表达式优缺点见上文,优点是形参参数可变,且支持包括运算符和运算对象的元素作为组合式嵌套),Scala 的静态类型导致参数长度可变很困难,高阶函数使用起来不自由,且动态嵌套运算符比较啰嗦:call(if (xxx) sum else sub, Array(1,2,3)) vs ((if (xxx) sum sub) 1 2 3),更多的是嵌套运算对象,而 Lisp 的这种特点,则完全来自于数据即过程的思想:因为过程即数据,因此运算符过程可以像数据一样灵活、动态操作,过程形参格式可以不受限制。 除此之外,传统写法和前缀表达式仅仅是函数括号在函数名前后的区别:iter(improve(make_guess(x,g))) vs. (iter (improve (make_guess x g)))。

过程所产生的计算
现在我们理解了过程抽象,但又并没有理解它。一个程序是一种模式,其描述了一个计算过程的局部演化方式,为了使用过程抽象来控制计算过程的进展,需要了解不同种类的过程抽象会产生什么样的计算过程(即了解一些简单过程产生的计算过程的“形状”,以及计算过程在时间和空间上对计算资源的消耗),之后才可能构造可靠的程序,使其表现出所需要的行为。这里所谓的形状,更多指的是程序执行的不同过程中各个表达式状态堆叠形成的表观路径:空间(堆栈)增长或收缩,比如下面所示的线性递归计算和线性迭代过程:
(define (factorial n)
;计算阶乘 n x (n-1) x (n-2) .. x 1,递归方式
(if (= n 1) 1
(* n (factorial (- n 1)))))
(define (factorial2 n)
;计算阶乘 1 x 2 x .. x (n-1) x n,迭代方式
(define (fact-iter now)
(if (= now n)
n
(* now (fact-iter (+ now 1)))))
(fact-iter 1))
(printf "fac:~s, fac2:~s" (factorial 10) (factorial2 10))

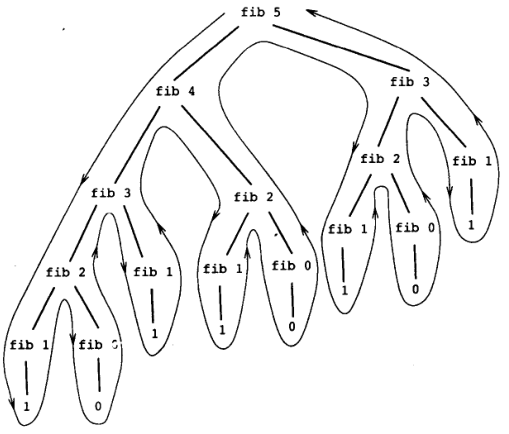
所谓递归,其指的就是此过程的定义中直接或间接的引用了此过程本身,而不同的递归方式,比如线性递归,指的就是计算过程的进展方式,而非语法表现形式,线性递归的例子如上所示,其相比较迭代 —— 迭代可以被看做一种特殊的递归,其不包含空间冗余和延迟计算,仅利用形参传递的动态性执行相同过程不同状态的遍历,效率还算 OK,只是空间利用率稍低。递归有一种特殊形式,即树状递归,树状递归试图表述的算法非常容易理解,但是性能又低的可怕,包含大量冗余计算,比如下图中计算斐波那契数列的 fib 过程。fib2 是一种计算斐波那些数列的另一种算法,使用了尾递归。这里要说明一点,不是所有的递归形式都占据大量空间,对于尾递归而言,其可以被优化为迭代,只是语法形式不同,效率不相上下,注意 LISP 并没有提供迭代的类似 C 的那种 for、do、while 控制结构,因为这是完全不必要的。
(define (fib n)
;树状递归的例子,大量的冗余计算出现
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 2)) (fib (- n 1))))))
(define (fib2 n)
;尾递归优化:且更改算法以避免树状冗余分支
(define (iter a b count)
(if (= count 0)
b
(iter (+ a b) a (- count 1))))
(iter 1 0 n))
现在考虑下面的问题: 给了半美元、四分之一美元、10美分、5美分和1美分的硬币,将1美元换成零钱,一共有多少种不同方式?更一般的问题是,给定了任意数量的现金,我们能写出一个程序,计算出所有换零钱方式的种数吗?这个问题可以充分展示出树状递归算法的简单性:现金 a 换为 n 种硬币的不同方式数目等于将 a 换位除第一种硬币外所有其他硬币的不同方式数目 + a - d 换成所有种类的硬币不同方式的数目,d 是第一种硬币的币值。考虑到边界条件,a 为 0 时,1 种方式,a < 0 时,0 种方式,n = 0 则 0 种方式。
(define (count-change amount)
(define (first-denomination kinds-of-coins)
;根据可用的硬币总数返回第一种硬币的币值
(cond ((= kinds-of-coins 1) 1)
((= kinds-of-coins 2) 5)
((= kinds-of-coins 3) 10)
((= kinds-of-coins 4) 25)
((= kinds-of-coins 5) 50)))
(define (cc amount kinds-of-coins)
(cond ((= amount 0) 1)
((or (< amount 0) (= kinds-of-coins 0)) 0)
(else (+ (cc amount (- kinds-of-coins 1))
(cc (- amount (first-denomination kinds-of-coins))
kinds-of-coins)))))
(cc amount 5))
(printf "kind of change ~s" (count-change 100))
对于 (count-change 11) 而言,其树状递归的形状大致如下所示,使用下文大 O 记法,大概是指数级别的时间和空间增长:

对于大部分问题,递归确实非常直观,符合人类直觉,而迭代则较难去构造,比如下面 n < 3, f(n) = n, n >= 3, f(n) = f(n-1) + 2f(n-2) + 3f(n-3) 这个问题,迭代需要保存三个中间变量(不保存当前 fn 值的原因是它很容易可根据等式计算出来,在满足条件时计算并返回,不满足条件时作为上一个 f(n-1) 计算并递归,这种方式可避免初始化时的 f(3) 计算。当然也可以保存,在初次调用时手工计算 f(3) 并传入,之后满足条件则直接返回此参数,不满足则作为当前 f(n) 进行计算,这两者只是 lazy call 和 eager call 的区别),加上条件判断的一个,这里和上面的斐波那契迭代类似却又不同,斐波那契那里的算法是 eager call,每次递归前都将最终结果构造好了。这里使用 lazy call 可使得代码更清晰。
(define (f n)
(if (< n 3)
n
(+ (f (- n 1))
(* 2 (f (- n 2)))
(* 3 (f (- n 3))))))
(define (f2 n)
(define (fa fnm3 fnm2 fnm1 mark)
(define fn (+ fnm1 (* 2 fnm2) (* 3 fnm3)))
(cond ((= mark n) fn)
(else (fa fnm2 fnm1 fn (+ mark 1)))))
(if (< n 3) n (fa 0 1 2 3)))
如下所示为帕斯卡三角形的计算方法,再次印证了:对于大部分问题,递归非常直观且容易理解:

通常使用大 O 记法(增长的阶)来衡量计算过程消耗计算资源的程度。另 n 为一个参数,R(n) 为计算过程处理规模为 n 问题需要的资源,这里的 n 可粗略来自于某个和问题相关的值,R(n) 可能为所用的指令数目(时间)或者使用的内部寄存器数目(空间)。称 R(n) 有 θ(f(n)) 的增长阶:R(n) = θ(f(n)),存在和 n 无关的两个整数 k1 和 k2 使得 k1f(n) <= R(n) <= k2f(n) 对任何足够大的 n 都成立。这里的 f(n) 一般为常数、平方、次方、指数,对于一个增长的阶为 θ(n2) 的计算过程,其可能实际需要 1000n2 步,或者需要 3n2 + 10n + 7 步,因此增长的阶是一种很粗略的描述,但也要看到它的价值:对于 θ(n) 线性计算过程,规模增大一倍所有资源增加一倍,而 θ(n2) 则对增加 1 就导致资源常数级增长,θ(logn) 则温和的多,问题规模增大,所需资源只增加一个常数。
下面是一个例子,计算 sineX 的值。在求值的时候, a 每次都被除以 3.0 ,因此当 a 增大 3 倍,实际才会多调用一次 p。介于 sine 是一个递归程序,因此它的时间和空间复杂度都比线性要低,为 O(loga)。
(define (sine angle)
;当角 x 足够小,sinx ≈ x,反之可通过 sinx = 3sin(x/3) - 4sin^3(x/3) 减小其参数大小
(define (cube x) (* x x x))
(define (p x)
(- (* 3 x) (* 4 (cube x))))
(if (not (> (abs angle) 0.1))
angle
(p (sine (/ angle 3.0)))))
(printf "sine 12.15 is ~d" (sine 12.15))
下面是一个例子,用来求 b 的 n 次幂,基于计算过程消耗的度量,下面这些不同的算法有不同的性能。特殊递归实现每次递归以 n/2 的速度下降,特殊迭代实现每次迭代以 n/2 的速度上升、
(define (expt1 b n)
;递归实现 θ(n) step and space
(if (= n 0) 1 (* b (expt1 b (- n 1)))))
(define (expt2 b n)
;迭代实现 θ(n) step, θ(1) space
(define (exp-inner m now)
(if (< m n) (exp-inner (+ m 1) (* now b)) now))
(exp-inner 0 1))
(define (expt3 b n)
;特殊递归实现 θ(logn) step and space
(define (square x) (* x x))
(define (even? n) (= (remainder n 2) 0))
(cond ((= n 0) 1)
((even? n) (square (expt3 b (/ n 2))))
(else (* b (expt3 b (- n 1))))))
(define (expt4 b n)
;特殊迭代实现 θ(logn) step and space
(define (even? n) (= (remainder n 2) 0))
(define (exp-inner a n)
(cond ((< n 2) a)
((even? n) (exp-inner (* a (* b b)) (/ n 2)))
(else (exp-inner (* a b) (- n 1)))))
(if (= n 1) b (exp-inner 1 n)))
下面是另一个类似的例子:使用加法实现了乘法,两种实现算法中,一种基于线性递归,每次 b 减 1 后加上一份 a,另一种基于对数(对数递归和对数迭代),每次 b 试图减一半,然后乘 2,如果失败后继续使用使用 b - 1,a 增加一倍的算法。这里对数迭代的方法又被称之为“俄罗斯农民的方法”,Rhind Pahyrus 的文章中可以找到。
(define (multi a b)
;乘法的基本递归形式:每次 b 下降 1,a 增加 1 倍,θ(n) steps
(if (= b 0) 0 (+ a (* a (- b 1)))))
(define (multi2 a b)
;乘法的高效递归形式:每次 b 下降一半,a 增加 2 倍,θ(logn) steps
(define (double x) (+ x x))
(define (halve x) (/ x 2))
(define (even? n) (= (remainder n 2) 0))
(cond ((= b 0) 0)
((even? b)
(double (multi2 a (halve b))))
(else (+ a (multi2 a (- b 1))))))
(define (multi3 a b)
;乘法的高效迭代形式:θ(logn) steps
(define (double x) (+ x x))
(define (halve x) (/ x 2))
(define (even? n) (= (remainder n 2) 0))
(define (multi-inner now-b now-a)
(cond ((< now-b 2) now-a)
((even? now-b) (multi-inner (halve now-b) (double now-a)))
(else (multi-inner (- now-b 1) (+ now-a now-b)))))
(multi-inner b a))
下面是斐波那契数列的树状递归、线性递归、线性迭代、对数迭代(Kaldewaij 1990)的分别实现方式。说实话,这里充分体现了递归,尤其是树状递归是如何的贴近于思维,而迭代,尤其是具有较小增长阶的迭代是如何闪耀着人类的智慧:充分印证了“计算机程序 = 算法 + 数据结构”这一说法。
(define (fib n)
;树状递归的例子,大量的冗余计算出现
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 2)) (fib (- n 1))))))
(define (fib2 n)
;尾递归优化:且更改算法以避免树状冗余分支
(define (iter a b count)
(if (= count 0)
b
(iter (+ a b) a (- count 1))))
(iter 1 0 n))
(define (fib3 n)
;斐波那契数列的线性迭代解决方法 2
;这种方法 a<-a+b, b<-a 称之为 T 变换, 将初始值为 n 的 count 的下降作为状态
;容易发现 T 变换 n 此将导致 Fib(n+1) 和 Fib(n)
(define (f-iter a b count)
(if (= count 0) b (f-iter (+ a b) a (- count 1))))
(f-iter 1 0 n))
(define (fib4 n)
;斐波那契数列的对数迭代解决方法
;在 f3 中的 T 变换本质上是 Tpq 变换族中 p=0,q=1 对于对偶 (0,1) 进行变换的特例。
;即 Tpq 是对于对偶 (a,b) 按照 a<-bq+aq+ap 和 b<-bp+aq 规则进行的变换。因为 Tpq 变换
;两次等价于一种特殊的 p q 值的应用,因此可以连续求平方的方式计算 Tn。
;计算过程非常简单,用 a1,b1,p,q 表示 a2,b2,用 a2,b2,p,q 表示 a3,b3
;然后将表示 a3,b3 的 a2,b2 代换为 a1,b1, 得到 a3,b3 和 a1,b1,p,q 的表示关系,最后
;对照 a3,b3 和 a1,b1,p',q' 的关系,即可得到 p-p' 以及 q-q' 的关系。
(define (even? n) (= (remainder n 2) 0))
(define (f-iter a b p q count)
(cond ((= count 0) b)
((even? count)
(f-iter a b (+ (* p p) (* q q)) (+ (* q q) (* 2 p q)) (/ count 2)))
(else (f-iter (+ (* b q) (* a q) (* a p))
(+ (* b p) (* a q))
p q (- count 1)))))
(f-iter 1 0 0 1 n))
最后,下面关于素数的例子生动形象的展示了过程抽象的三重意义:思维过程的隔离、过程结果的重用以及代码复用(过程抽象模板的使用)以及过程所产生计算的形状,提供了一种性能测试工具,以衡量不同算法(暴力算法、费马小定理、基于 Miller-Rabin 检查的费马小定理)的正确性以及不同算法、抽象方式以及数据规模对过程性能产生的微妙影响 —— 一言以蔽之,增长阶实际不会表现出理论的性能差异,除非数据量巨大。
(define (prime? n)
;一种直接寻找素数的方法:从 2 开始去除,直到 √n 为止,
;原因很简单,如果 d 是 n 的因子,则 d/n 也是,d 和 d/n 都不会大于 √n
;2 - √n 返回内找不到则返回 n 表示为素数。有 θ(√n) 的增长阶
(define (square x) (* x x))
(define (divides? a b) (= (remainder b a) 0))
(define (find-divisor n test)
(cond ((> (square test) n) n)
((divides? test n) test)
(else (find-divisor n (next test)))))
;如果不能被 2 整除,那么后续所有偶数都不需要检验了
;(define (next n) (if (= n 2) 3 (+ n 2)))
(define (next n) (+ n 1))
(define (smallest-divisor n)
(find-divisor n 2))
(= n (smallest-divisor n)))
(define (prime?2 n)
;基于费马小定理计算素数:若 n 为素数,a 为小于 n 正整数,则 a^n与a “模n同余”。
;对小于 n 的正整数 a,尝试 a^n mod n, 如果不等于 a,那么肯定不是素数,反之则继续尝试
;注意,存在非素数满足 a^n与a 模n同余,不过概率很小。
(define (even? x) (= (remainder x 2) 0)) ;过程抽象的分割性
(define (square x) (* x x)) ;过程抽象的值重用性
(define (expmod base exp m) ;过程抽象的过程重用性
;计算 base^exp mod m 的值,使用连续求平方的方式对数增长阶计算
;注意,这里并不直接 (reminder (expt base exp) m) 的原因是大数量级效率更高
(cond ((= exp 0) 1)
((even? exp)
;一种更低效的实现将 square 换成 *, 注意更换后表达式会被计算两遍,
;如果不想计算, 使用定义- define 值,或者过程定义- square。
(remainder (square (expmod base (/ exp 2) m)) m))
(else (remainder (* base (expmod base (- exp 1) m)) m))))
(define (fermat-test n)
;随机从小于 n 的数中找一个正整数执行计算
(define (try-it a) (= (expmod a n n) a))
(try-it (+ 1 (random (- n 1)))))
(define (fast-prime? n times)
;尝试 times 次,如果其中之一得到 false 结果即返回,反之返回 true
(cond ((= times 0) #t)
((fermat-test n) (fast-prime? n (- times 1)))
(else #f)))
(fast-prime? n 10))
(define (prime?3 n)
;基于 Miller-Rabin 检查避免 carmichael 数
;对于素数 n,小于 n 的整数 a 的 (n-1) 次幂与 1 模 n 同余
(define (even? x) (= (remainder x 2) 0))
(define (square x) (* x x))
(define (expmod base exp m)
(define (nontrivial-square-root?) ;素数 a^2 mod n != 1
(and (not (= base 1))
(not (= base (- m 1)))
(= 1 (remainder (square base) m))))
(cond ((= exp 0) 1)
((nontrivial-square-root?) 0) ;检验失败则返回 0 表示非素数
((even? exp)
(remainder (square (expmod base (/ exp 2) m)) m))
(else (remainder (* base (expmod base (- exp 1) m)) m))))
(define (non-zero-random n) ;一个不为 0 的随机数,小于 n
(define r (random n))
(if (not (= r 0)) r (non-zero-random n)))
(define (fast-prime? n times)
;至少尝试 n/2 次,可保证绝对没有 carmichael 数
(cond ((= times 0) #t)
;Miller-Rabin 核心:素数的 a^(n-1) mod n = 1
((= (expmod (non-zero-random n) (- n 1) n) 1)
(fast-prime? n (- times 1)))
(else #f)))
(fast-prime? n (ceiling (/ n 2))))
(printf "prime1?5 ~s prime1?15 ~s\n" (prime? 5) (prime? 15))
(printf "prime2?5 ~s prime2?15 ~s\n" (prime?2 5) (prime?2 15))
(printf "prime3?5 ~s prime3?15 ~s\n" (prime?3 5) (prime?3 15))
(define (carmichael-find-in n)
;计算 2 - n 内的 carmichael 数 - 即费马小定理失效的数
;并检验 Miller Rabin 测试是否通过
(define (print-if-find n)
(printf "Carmichael number: ~4d, Miller-Rabin check ~d\n"
n (prime?3 n)))
(define (look-for-primes now max)
(define prime-no-fima (prime? now))
(define prime-fima (prime?2 now))
(if (and prime-fima (not prime-no-fima)) (print-if-find now))
(if (< now max) (look-for-primes (+ now 1) max)))
(look-for-primes 2 n))
(carmichael-find-in 10000)
(define (search-for-primes n)
;查找 2 - n 范围内所有的素数
(define (timed-prime-test n)
;进行素数寻找
(start-prime-test n (time-nanosecond (current-time))))
(define (start-prime-test n start-time)
;调用素数函数 prime? 进行实际查找
(if (prime? n) (report-prime n
(- (time-nanosecond (current-time)) start-time))))
(define (report-prime n elapsed-time)
;打印查找耗时
(printf "\n~s" n)
(display " *** ")
(display elapsed-time))
(define (look-for-primes now max)
(timed-prime-test now)
(if (< now max) (look-for-primes (+ now 1) max)))
(look-for-primes 2 n))
;(search-for-primes 10000)
使用高阶函数做抽象
当我们不理解一种抽象的价值或者没有为其找到典型的应用时,往往会认为这种形式是多此一举。比如在本章开头,对于 + - * / 这些基本运算包装到黑盒中作为基本过程抽象一样,繁琐并且参数传来传去,也很麻烦。现在我们提出一种基于“基本过程抽象”之上的抽象:基本过程抽象仅以数作为参数,这限制了模板的抽象能力,考虑让过程作为参数或者作为返回值,那么过程抽象的抽象表述能力将极为增强。这种操作过程的过程被称之为“高阶过程”。
作为参数的过程
下面这三个问题都能使用 sum-? 的高阶过程进行表示,基于此高阶过程,我们重新定义了复用此高阶过程的基本过程。这里看上去变复杂了,但要看到,随着高阶过程越来越复杂,或者需要不断演进,那么这种依赖高阶过程的问题就可以仅实现或修改高阶过程来一次性的解决所有问题,但也要敏锐的看到,试图抽象出这种高阶过程本身就是极困难的一件事(换言之,①对于高阶过程本身:高阶过程提供了一种过程依赖的更为抽象和通用的演化方式)。此外,②对于试图解决的问题:高阶函数提供了一种思考的模式识别模板,以试图划归和解决同一类问题。上述这两点是交替进行的,高阶函数的抽象和演化动力往往来自于试图将更多相似问题纳入同一抽象的努力。
(define (sum-integers a b)
;计算 a + .. + b
(if (> a b) 0 (+ a (sum-integers (+ a 1) b))))
(define (sum-cubes a b)
;计算 a^3 + .. + b^3
(define (cube x) (* x x x))
(if (> a b) 0 (+ (cube a) (sum-cubes (+ a 1) b))))
(define (sum-pi a b)
;计算 1/(1*3) + 1/(5*7) + 1*(9*11) + ...
(if (> a b) 0 (+ (/ 1.0 (* a (+ a 2))) (sum-pi (+ a 4) b))))
(define (sum-? left-compute left-generate a b)
;基于线性递归的实现
(if (> a b) 0 (+ (left-compute a)
(sum-? left-compute
left-generate
(left-generate a) b))))
(define (sum-?2 left-compute left-generate a b)
;基于线性迭代的实现
(define (iter a result)
(if (> a b) result (iter (left-generate a)
(+ result (left-compute a)))))
(iter a 0))
(define (sum-integers2 a b)
(define (identity a) a)
(define (plus-one a) (+ a 1))
(sum-? identity plus-one a b))
(define (sum-cubes2 a b)
(define (cube a) (* a a a))
(define (plus-one a) (+ a 1))
(sum-? cube plus-one a b))
(define (sum-pi2 a b)
(define (pi-compute a) (/ 1.0 (* a (+ a 2))))
(define (pi-produce a) (+ a 4))
(sum-? pi-compute pi-produce a b))
(printf "i ~d c ~d p~d\n" (sum-integers 1 100) (sum-cubes 1 10) (sum-pi 1 10))
(printf "i2 ~d c2 ~d p2 ~d\n" (sum-integers2 1 100) (sum-cubes2 1 10) (sum-pi2 1 10))
上述这三个问题使用基本过程定义也能很好的解决,注意使用高阶过程后代码反而变得复杂了 —— 虽然这里可以将 plus-one 函数在 sum-integers2 和 sum-cubes2 之间重用,但总体付出大于回报。但如果将更多、更复杂的问题纳入思考的话,比如下面求解 f 在 a b 之间的定积分过程,高阶函数提供的抽象能力就能够为我们解决问题提供一种方便的框架了,尤其是使用吉普森规则计算的时候表现的更为明显:这里的计算公式和 sum-? 高阶抽象之间差距稍大,需要仔细定义变换:
(define (integral f a b dx)
;使用高阶过程求解 f 在 [a,b] 之间的定积分,精度为 dx
;其可以看做 [ f(a+dx/2) + f(a+dx+dx/2) + f(a+2dx+dx2) + ..] dx
(define (add-dx x) (+ x dx))
(* (sum-? f add-dx (+ a (/ dx 2.0)) b) dx))
(define (integral2 f a b n)
;吉普森规则计算数值积分,f 在 [a,b] 的定积分是
;(h/3)[y0 + 4y1 + 2y2 + 4y3 + 2y4 + .. + 4y(n-1) + yn]
;其中 h = (b-a)/n,n 为某个偶数,增大 n 能提高近似的精度
;其中 yk = f(a + kh)
(define h (/ (- b a) n))
(define (computeOld k)
(define (y) (f (+ a (* k h))))
(define (even?) (= (remainder k 2) 0))
(cond ((or (= k 0) (= k n)) (y))
((even?) (* 2 (y)))
(else (* 4 (y)))))
(define (produceNew k) (+ k 1))
(* (/ h 3.0) (sum-? computeOld produceNew 1 n)))
(define (cube x) (* x x x))
(printf "integral ~d ~d\n" (integral cube 0 1 0.01) (integral2 cube 0 1 100))
(printf "integral ~d ~d\n" (integral cube 0 1 0.001) (integral2 cube 0 1 1000))
【两个简单认识】上面提到,高阶函数的两个作用,其一是为依赖高阶抽象的过程提供一个统一修改的位点,提供一种渐进的程序演化方式,其二是在解决新问题的时候作为一种思维的模板,试图划归问题。下面展示了高阶函数的这种“思维模板”的作用,以及当目前的模板和解决问题所需不匹配时,我们创建新的高阶函数抽象过程模板的方法。这里的问题是求 π 的值,为了高阶函数抽象过程,先要找出问题的基本过程,然后循序渐进的从中寻求规律,这里的 factorial 基本过程提供了一个例子。可以看到,product 是过程抽象为高阶函数的极好位置,但是这里无法匹配上面抽象的模板:sum-?,因此我们提出一个类似的 product-? 高阶函数抽象,如下所示。
(define (factorial)
;使用 π/4 = 2*4*4*6*6*8../3*3*5*5*7*7.. 计算 π 的值
(define (product from to)
(cond ((< from to)
(* (/ (* from (+ from 2)) (* (+ from 1) (+ from 1)))
(product (+ from 2) to)))
(else 1.0)))
(* 4 (product 2 1000)))
(define (product from to from-fun from-gen)
(cond ((< from to)
(* (from-fun from) (product (from-gen from) to from-fun from-gen)))
(else 1.0)))
(define (factorial2)
(define (from-fun x) (/ (* x (+ x 2)) (* (+ x 1) (+ x 1))))
(define (from-gen x) (+ x 2))
(* 4 (product 2 1000 from-fun from-gen)))
(printf "π is ~d ~d\n" (factorial) (factorial2))
【一个新的抽象】根据洛克对人类思维的观点,我们这里在“sum-?”这个简单认知外,又具备了 “product-?”这个简单认知,当然,下一步就是将两个简单认知合并,形成一个复杂认知,这就是 “accumulate”,这里抽象的东西很自然:运算符 combiner 以及初始值 null-value,对于 term、next 则是高阶函数 sum-? 和 product-? 中已经进行的抽象,分别代表了对旧值的计算和通过旧值生成新值的方法。如下所示基于高阶函数建立了两层抽象,accumulate 位于最底层,sum 和 product 位于中层,而实际问题则位于最上层。
(define (accumulate combiner null-value term a next b)
(cond ((< a b)
(combiner (term a)
(accumulate combiner null-value term (next a) next b)))
(else null-value)))
(define (sum-by-accumulate term a next b)
(accumulate + 0.0 term a next b))
(define (product-by-accumulate term a next b)
(accumulate * 1.0 term a next b))
(define (factorial-by-accumulate)
(define (term x) (/ (* x (+ x 2)) (* (+ x 1) (+ x 1))))
(define (next x) (+ x 2))
(* 4 (product-by-accumulate term 2 next 1000)))
(define (sum-cube-by-accumulate a b)
(define (cube x) (* x x x))
(define (next x) (+ x 1))
(sum-by-accumulate cube a next b))
(printf "π ~d, sum of 1^3 to 10^3 ~d\n"
(factorial-by-accumulate) (sum-cube-by-accumulate 1 10))
【合并了的认识】第三次强调,高阶函数的两个作用,其一在于为低级过程提供统一修改位点,提供一种代码复用和渐进的程序演化方式,其二在于为新问题提供思维模板。这两者是交互作用的,如果问题无法使用旧有思维模板,那么我们将提出新的思维模板,新的模板作为一种新的简单认知,可以合并、对照和重新抽象为新的普适的思维模板(即洛克认为的复杂思维产生的三个步骤:合并、对照和抽象)。上面基于抽象的二层抽象(高阶函数的高阶函数)就证明了这一点。而随着需要解决的新问题源源不断的出现,我们不断重复这个步骤:产生新认识、合并多个认识、对照多个认识、形成新的抽象。这就是高阶函数两个目的之间的交互作用。对于下面这两个问题:求 a - b 范围内所有素数之和、求小于 n 的所有和 n 互素的正整数,当我们分析问题的时候,发现它们和 accumulate 这一抽象的抽象的相似性,这里并不需要基于 accumulate 做新的抽象(也不能),而是互相对照后形成了新的抽象:filtered-accumulate(可以看一个增强版本),如下所示:
(define (filtered-accumulate combiner null-value term a next b filtered)
(cond ((< a b)
(if (filtered a)
(combiner (term a)
(filtered-accumulate combiner
null-value
term (next a) next b))
(filtered-accumulate combiner
null-value
term (next a) next b)))
(else null-value)))
(define (prime-sum a b)
;基于 filtered-acc 实现的求 a-b 范围内所有的素数之和
(define (identity x) x)
(define (next x) (+ x 1))
(define (prime? n) ??? )
(filtered-accumulate + 0 identity a next b prime?))
(define (prime-product n)
;基于 filtered-acc 实现的求小于 n 的所有和 n 互素的正整数:GCD(i,n)=1 之积
(define (identity x) x)
(define (next x) (+ x 1))
(define (gcd a b) (if (= b 0) a (gcd b (remainder a b))))
(define (gcd-good? x) (= (gcd x n) 1))
(filtered-accumulate * 1.0 identity 1 next n gcd-good?))
用 lambda 构造过程
在上述高阶函数使用的过程中,我们发现,对传入高阶函数参数频繁定义过程,大部分都还是很简单的过程是一件枯燥的事情。Scheme 包含了一种特殊形式,允许我们使用 lambda 构造匿名过程,lambda 和过程定义的语法一致,除了不包含名字:(lambda (
如果说 lambda 表达式是 define procedure 省略了过程名,那么 let 表达式则是 lambda 语法的简单形式(语法糖)。let 表达式主要用于提供一种变量上下文,在其作用域内可方便的使用这些变量。其形式为 (let ((key1 value1) (key2 value2) (key3 value3)) <body here>),等价于 ((lambda (key1 key2 key3) <body here>) value1 value2 value3)。因为 let 本质就是 lambda,因此有一些需要注意的问题:①let 绑定的变量本质是 lambda 形参的外部传入,如果其作为值,则值为外部绑定,而非上一个同名变量:假设 x = 3, (let ((x 5) (y x)) (display y)) 中打印的结果为 3 而不是 5。②lambda 表达式有返回值,这很自然,过程都有返回值,而 let 作为 lambda 的语法糖,也有返回值:(+ 5 (let ((a 5)) a)) 的值为 10。
lambda 本质上可以使用“定义过程”替换,let 本质上可以使用“定义”替换,正如我们之前在过程抽象中做的那样:对于局部变量使用 define x 来定义,对于局部过程使用 define (x) 来定义。对于比较短小的过程定义,完全可以使用 lambda 替代,这可以简化高阶函数的使用,而对于 let,相比较 define 局部变量,let 的优点在于更细化的局部变量作用域范围,这意味着更紧凑的代码和更好的模块化 —— 虽然我们使用内部定义来隐藏局部变量可见性,但是如果一个过程很长,那么内部定义最终也会像全局变量一样乱糟糟的,而使用 let 来应对短生命周期局部变量则可以充分避免这种问题(类似于 JavaScript 的 with,Kotlin 的 with 但目的不一致)。因此在过程内部,一般使用 let 在定义短生命周期变量,define 在内部定义长声明周期变量和过程,lambda 用于作为高阶函数的参数或返回值传递。
下面是一个例子:
(define (half-interval-method f a b)
;折半法寻找 f(x)=0
(define (search f neg pos)
(define avg (lambda (x y) (/ (+ x y) 2)))
(define close? (lambda (neg pos) (< (abs (- neg pos)) 0.001)))
(let ((mid (avg neg pos)))
(if (close? neg pos) mid
(let ((test (f mid)))
(cond ((positive? test) (search f neg mid))
((negative? test) (search f mid pos))
(else mid))))))
(let ((a-value (f a))
(b-value (f b)))
(cond ((and (negative? a-value) (positive? b-value))
(search f a b))
((and (negative? b-value) (positive? a-value))
(search f b a))
(else (error "Values are not of opposite sign" a b)))))
(printf "sin ~d\n" (half-interval-method sin 2.0 4.0))
(printf "~d\n" (half-interval-method (lambda (x) (- (* x x x) (* 2 x) 3)) 1.0 2.0))
过程作为一般性的方法
下面包含了两个例子:函数不动点以及无限连分式,以及其在一些数学问题的应用。这些例子反映了上述提到的大部分内容:定义与过程抽象、递归 & 迭代对于过程抽象的应用、过程作为参数的高阶函数、lambda 表达式与 let 表达式在高阶函数中的应用。
(define (fixed-point f first-guess)
;求解不动点 f(x)=x 方法:不断的将 f(x) 作为 f 的输入,直到得到容忍度内结果
(define tolerance 0.00001)
(define (close? v1 v2) (< (abs (- v1 v2)) tolerance))
(define (try guess)
(let ((next (f guess)))
(if (close? guess next) next (try next))))
(try first-guess))
(printf "~d ~d ~d\n"
(fixed-point cos 1.0)
(fixed-point (lambda (y) (+ (sin y) (cos y))) 1.0)
(fixed-point (lambda (x) (+ 1 (/ 1 x))) 1.0)) ;黄金分割点可以使用不动点计算
不动点可用来计算 sqrt,但是直接计算 lambda (y) (/ x y) 有问题,因为会出现震荡,即值不断的在 sqrt 的 lambda 函数周围摇摆,因此需要一个阻尼函数 lambda (x) (/ (+ x (f x)) 2) 来温和化:
(define (sqrt x)
(define sqrt-f (lambda (y) (/ x y)))
(fixed-point sqrt-f 1.0))
(define (average-damp f) (lambda (x) (/ (+ x (f x)) 2)))
(define (sqrt-2 x)
(define sqrt-f (lambda (y) (/ x y)))
(fixed-point (average-damp sqrt-f) 1.0))
使用阻尼函数还可以简化不动点的迭代/递归所需步骤:
(define formula (lambda (x) (/ (log 1000) (log x))))
(fixed-point formula 2.0)
(fixed-point (average-damp formula) 2.0)
下面展示了一个无穷连分式和 k 项有限连分式的形式,有特殊形式,当 Nk = 1 且 Dk = 1 时,k 项有限连分式返回 1/黄金分割点 的值,下面展示了递归计算和迭代计算黄金分割点的过程:

(define (cont-frac n d k)
;计算 k 项有限连分式:N1 / (D1 + (N2 / (D2 + (N3 / (D3 + ...)))))
(define (cont-inner i)
(cond ((> i k) 0.0)
(else (/ (n k) (+ (d k) (cont-inner (+ i 1)))))))
(cont-inner 1))
(define (cont-frac-iter n d k)
;递归方式计算 k 项有限连分式:从 Nk 和 Dk 的商开始倒推
;依次往前加 d(k-1) 然后被 n(k-1) 除
(define (cont-inner i result)
(if (= i 0) result (cont-inner (- i 1) (/ (n i) (+ (d i) result)))))
(cont-inner (- k 1) (/ (n k) (d k))))
(define (cont-frac-1 k)
;当 Ni 和 Di 都为 1 时,k 项有限连分式会逼近 1/golden-ratio
(cont-frac-iter (lambda (i) 1.0) (lambda (i) 1.0) k))
(printf "~d\n" (cont-frac-1 100))
对于 e 自然对数而言,欧拉发现,Ni 为 1,Di 为 1 2 1 1 4 1 1 6 1 1 8 规律的序列的 k 项有限连分式返回的结果 + 2 等于 e,下面是求解 e 的实现:
(define (compute-e)
;根据欧拉 De Fractionibus Continuis 文中发现的:Ni 为 1,
;Di 为 1 2 1 1 4 1 1 6 1 1 8 的连分式求 e - 2
(+ 2.0 (cont-frac-iter
(lambda (i) 1.0)
(lambda (i)
(if (= (remainder i 3) 2)
(* 2 (+ 1 (floor (/ i 3))))
1))
1000)))
(printf "e is ~d\n" (compute-e))
对于 tan x,x 为弧度,Lambert 发现,可以使用如下规律的 k 项有限连进行计算:
(define (tan-cf x k)
;基于 Lambert 公式计算正切函数近似值
;tanx = x / (1 - x^2 / (3 - x^2 / (5 - ..)))
(define pow-x (* x x))
(cont-frac-iter (lambda (i) (- (* 2.0 i) 1))
(lambda (i) (if (= i 1) x pow-x))
k))
(printf "tan 30 is ~d" (tan-cf 30 1000))
过程作为返回值
一般而言,将程序设计语言中的“第一级”元素(一等公民)定义为带有最少限制的元素,其:①可以使用变量命名;②可以提供给过程作为参数;③可以作为过程的结果返回;④可以包含在数据结构中。Lisp 的过程是第一级元素,换言之,函数是一等公民。
上述例子(见下文)中的 average-damp 是一个过程作为参数且返回了过程的高阶函数。而这个返回过程的过程的抽象位置很好,这决定了其可复用性很高,对于任何需要利用 fixed-point 的函数,都可以将传入 fixed-point 的 f 套一层 average-damp 以避免震荡,提升阻尼。这是返回过程的高阶函数作为另一个过程运算对象的用例。如果说一般过程是一根静态水管,传入过程的过程是一根可根据传入模块实现动态过程的水管,那么返回过程的过程就是动态构造这种模块的水管,即传入模块的过程是动态的,传入的模块本身也是动态构造出来的。注意,这里的抽象和 FP 中 filter/map 的那种水管的抽象变换不同,这里强调的是命令式编程中过程的变换,而非 FP 那种对于数据的变换(Lisp 当然也能实现对数据的抽象和变换,见下一章节),如下图所示。
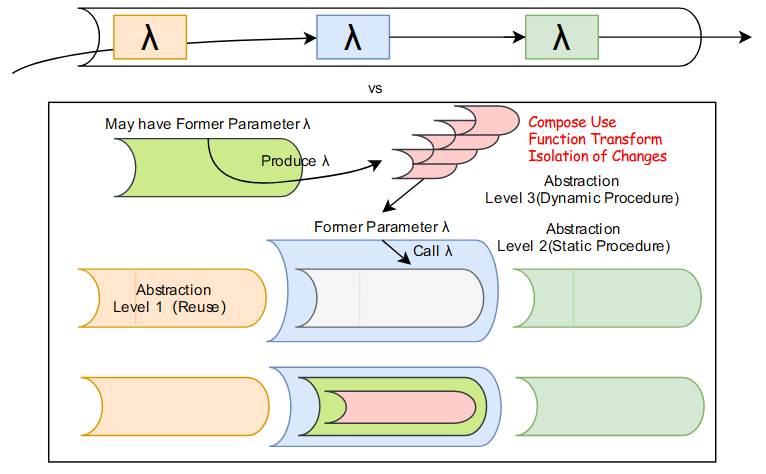

生产过程的过程和普通定义的过程之间存在微妙的区别:前者意味着更高的抽象,后者更具体。compose 用于对 f 和 g 函数进行叠加,我们很容易写成 compose2 的形式。虽然这两者生产的过程本质是一样的,但 compose1 更贴近心智模型:compose1、f、g 是等价的、平级的关系,其含义为 compose1 是 f 和 g 的组合,它们都是函数,而 compose2 则位于 f 和 g 更下的层级(更具体),其含义为 compose 函数依赖于 f 和 g 这两个过程作为参数。下面 repeated 函数:将 f 嵌套应用 n 次则更加深刻的反映了这一区别:repeated1 可以看做 f 的一种纯数学变换,repeated2 则是依赖 f 过程的一个更具体的外部过程。总的来说,作为返回值的过程并不是原始过程的一部分,这种和原始过程的分离意味着它不是一种“认识的组合”而是一种“抽象的新认识”,一种全新的抽象。
(define (compose1 f g) (lambda (x) (f (g x))))
(define (compose2 f g x) (f (g x)))
(printf "~d\n" ((compose1 (lambda (x) (* x x)) (lambda (x) (+ x 1))) 6))
(define (repeated1 f n)
(lambda (x)
(define (repeated n)
(if (= n 1) (f x) (f (repeated (- n 1)))))
(repeated n)))
(define (repeated2 f n x)
(if (= n 1) (f x) (f (repeated f (- n 1)))))
(printf "~d\n" ((repeated1 (lambda (x) (* x x)) 2) 5))
smooth 是一种依赖 repeated 的通过多次重复调用 fs 以对函数进行平滑的变换,如下所示,这里的终点在于我们看到了“生产过程”的过程是可以组合和嵌套的:repeated 和 smooth,组合嵌套后仍然保持了原来的抽象。
(define (smooth f n)
;对于函数 f(x) 的平滑定义为 f(x-dx), f(x) 和 f(x+dx) 的平均值, dx 为很小值
;本函数可以对 f(x) 进行 n 次平滑
(define dx 0.001)
(define fs (lambda (x) (/ (+ (f (- x dx)) (f x) (f (+ x dx))) 3)))
(define (repeated f n)
(lambda (x)
(define (repeated-inner n)
(if (= n 1) (f x) (f (repeated-inner (- n 1)))))
(repeated-inner n)))
(repeated fs n))
如果说将过程作为参数,在过程中调用这些作为参数的过程这一行为扩宽了过程抽象模板的问题适用性(适用性并非一上来就定义好的,而是随着时间不断变化的过程:通常在试图解决问题的时候,提出类似抽象过程,将多个抽象过程修改合并,比如 accumulate-? 或提供新的抽象,比如 filter-accumulate-? 对过程的这些修改动态的增强了抽象模板的问题适用性),那么将过程作为返回值进一步增强了过程抽象的能力:“将过程作为参数”仅仅是一个“将过程看做数据”的萌芽,其只是应用作为数据的过程,但并没有达到“从过程操纵数据到从过程操纵过程”的本质转变,而“将过程作为返回值”则通过更高的抽象淋漓尽致的展现了“将过程看做数据,用过程操作过程”的表达能力。这种高阶的抽象不仅可以实现②“操纵函数(过程)”的需求,还可以基于①不断叠加的抽象进行过程的同层级组合,并且在通过这种组合产生的抽象层次中③实现对于可变性的隔离。如果说函数是 Level 1 的抽象:过程重用和基于形参数据的动态过程,作为参数的函数是 Level 2 的抽象:基于形参过程的更灵活的动态过程,那么作为返回值的函数则是 Level 3+ 的抽象:Level1 和 Level2 的过程都是对数据的变换,而 Level3 则将过程看做数据,这种观念的转化有着极其深远的影响 —— 这意味着可以从多维而非平面维度上处理过程。一言以蔽之,生产过程的过程是通往无限抽象之门,按照洛克对认识的观点,我们可以在任意抽象层次进行认识的组合、认识的对照映射变换、定义当前抽象层级(大部分代码位于 Level1,少部分位于 Level2,极少数位于 Level 3+)。
上面对于“将过程作为返回值”的论断并不容易直接理解,但其可以轻松的由洛克认识论通过推理得到:假设生产过程的过程作为一种简单认识,那么我们首先试图将这些“生产过程的过程”组合就能发现这种抽象可以 ①将简单过程组合为复杂过程且保持组合前后抽象层级一致:区别于基本过程组合 (define (produce-add) (produce1) (produce2)),这里组合后的过程和其简单组件位于同一抽象层次,比如下文中的 double,double 怎么用,(double (double double)) 就怎么用。其次我们将这些“生产过程的过程”互相对比就能发现,这种过程本质上是②对过程而非数据进行的操控:过程是对数据进行的操控和变换,而当过程本身作为数据,则对过程的变换就依赖于“过程作为返回值”的高阶函数才可以做到,比如上文的 compose、repeat、smooth,虽然在一些情况下我们可以将问题转换为对数据操控的过程:compose1 和 repeat1,但有些时候不能:newton-transform 因为需要在 fixed-point-of-transform 中作为“对函数过程操控的过程”进行传入。最后将这种过程和基本过程、过程作为入参的高阶过程、生产过程的过程、组合了的生产过程的过程进行比较可以发现: ③在逐层抽象的过程中,实现的不同抽象层级,可供灵活使用并对可变性进行隔离,比如下文的 iterative-improve,这里的 guess 是一个更容易变化的值,相比较其他两个函数而言,这里虽不需要对过程进行操控,但是使用“过程作为返回值”的高阶函数,可以方便我们灵活使用抽象层次,并对可变性进行隔离。Scala 的 def xxxx(a:Double)(d:String)(e: ExecuteContext) 就是一个很好的例子,每层抽象捕获一个变量,其中内层抽象的变量更稳定,外层更不稳定,这种结构方便应对软件开发中不断变化的需求且保证核心不受影响。
【①过程组合】可能上述应用的“抽象性”体现的不太明显。但下面的例子中,被生成过程的抽象性则体现的淋漓尽致:作为运算符的过程动态生成并叠加:如下所示 double 为将 f 过程应用两次的过程,对于 inc 而言,其递增 2 而非 1,而对于下面这个 (double (double double)) 而言,就是一个持续叠加高阶函数的过程,理解并不复杂,套过程定义直接展开,在这里展开后是: (f (f (f (f (f (f (x)))))),最里面的 f 是 inc,之后依次是 2^0 .. 2^4 是 16,因此最后结果为 5 + 16 = 21。
(define (double f)
(lambda (x) (f (f x))))
(printf "~d\n" ((double (lambda (x) (+ x 1))) 1)) ; 3
(printf "~d\n" (((double (double double)) (lambda (x) (+ x 1))) 5)); 21
这里提供了一个完整的,使用牛顿法而非 average-damp 阻尼函数来求解不动点的例子。这个例子的意义在于:牛顿法过程中的 deriv、neutron-transform 和 average-damp 一样,都是一种将函数映射为新函数的抽象,因此比较适合“生产过程”的高阶函数来实现,虽然使用基本函数也可以,但并不平级,思维上有隔阂。
传统使用 average-damp transform 函数应用 fixed-point 的过程:
(define (fixed-point f first-guess)
;求解不动点 f(x)=x 方法:不断的将 f(x) 作为 f 的输入,直到得到容忍度内结果
(define tolerance 0.00001)
(define (close? v1 v2) (< (abs (- v1 v2)) tolerance))
(define (try guess step)
(let ((next (f guess)))
(if (close? guess next) next (try next (+ 1 step)))))
(try first-guess 1))
(define (average-damp f) (lambda (x) (/ (+ x (f x)) 2)))
(define (sqrt-1 x) (fixed-point
(average-damp (lambda (y) (- (* y y) x)) 1.0)
1.0))
使用牛顿法来 transform 函数并应用 fixed-point 的过程:
(define (neutron-method g guess)
;牛顿法是一个包含 g 函数的 f 函数:
;f(x)=x-(g(x)/Dg(x)), 其中 Dg(x) 为 g 对 x 的导数
;对此 f 函数求不动点将得到 g(x) = 0 的一个解
(define dx 0.00001)
;导数本质是返回函数的函数,Dg(x)=(g(x+dx) - g(x))/dx, dx 为很小的数
(define (deriv g) (lambda (x) (/ (- (g (+ x dx)) (g x)) dx)))
(define (neutron-transform g)
(lambda (x) (- x (/ (g x) ((deriv g) x)))))
(fixed-point (neutron-transform g) guess))
(define (sqrt-2 x) (neutron-method (lambda (y) (- (* y y) x)) 1.0))
【②函数变换】介于这两种方式之间存在着共性:均基于某种 transform 并应用 fixed-point,因此可以基于“高阶函数作为参数”来抽象,并基于此抽象来解决问题。要注意,实际上刚性的有这种直接需求“动态生产过程”的场景不多 —— 比如这里对过程(函数)应用过程:average-damp 和 neutron-transform,大部分情况下对数据的变换 - Level1,或者需要过程模板普适化,增强适用性 - Level2 更多。
(define (fixed-point-of-transform g transform guess)
(fixed-point (transform g) guess))
(define (sqrt-damp x) (fixed-point-of-transform (lambda (y) (/ x y))
average-damp 1.0))
(define (sqrt-newton x) (fixed-point-of-transform (lambda (y) (- (* y y) x))
newton-transform 1.0))
最后的这个例子说明了我们是如何抽象出“逼近并检查”这一过程的,这里的 iterative-improve 是一个 Level3 层次的抽象,注意,这种抽象比 Level2(之前的 accumulate-?困难的多)。
(define (fixed-point f first-guess)
;求解不动点 f(x)=x 方法:不断的将 f(x) 作为 f 的输入,直到得到容忍度内结果
(define tolerance 0.00001)
(define (close? v1 v2) (< (abs (- v1 v2)) tolerance))
(define (try guess step)
(printf "step:~d value:~d\n" step guess)
(let ((next (f guess)))
(if (close? guess next) next (try next (+ 1 step)))))
(try first-guess 1))
(define (cube x)
(define (is-good-cube x g)
(< (/ (abs (- x (* g g g))) x) 0.01))
(define (improve-cube x g)
(guess-cube x (/ (+ (/ x (* g g)) (* g 2)) 3)))
(define (guess-cube x g)
(if (is-good-cube x g) g (improve-cube x g)))
(guess-cube x 1.0))
(define (iterative-improve is-good? improve)
(lambda (first-guess)
(define (iter guess)
(define next (improve guess))
(if (is-good? guess next) x (iter next)))
(iter first-guess)))
(define (fixed-point-by-ii f first-guess)
(define tolerance 0.00001)
(iterative-improve
(lambda (guess next) (< (abs (- guess next)) tolerance))
(lambda (guess) (f guess)) first-guess))
(define (cube-by-ii x)
(iterative-improve
(lambda (guess next) (< (/ (abs (- x (* guess guess guess))) x) 0.01))
(lambda (guess) (/ (+ (/ x (* guess guess)) (* guess 2)) 3))
1.0)
【③隔离可变性】这里引出了一个有意思的问题,抽象到 L2:(iterative-improve is-good? improve first-guess) 和 L3:(iterative-improve is-good? improve) (lambda (first-guess) xxx) 的区别是什么?我们现在清楚后者是一种更高级的抽象,其更加困难,而这种困难不是我们人为设置的障碍,而是一种对于“变化”和“不变”进行区分的要求导致的:L3 的抽象可以将一个过程区分为几个不同的抽象层次,就像“过程抽象”将一个过程区分为几个不同的步骤一样。生成过程的过程为我们提供了不同层次的抽象,以便我们更加方便的调用 —— 如果不这样,那么每次依赖最高层抽象时都需要传递大量参数,非常繁琐。比如上面的例子,first-guess 相比较 is-good? 和 improve 这两个参数,很显然变化的概率大得多,因此和这两个过程 is-good? 和 improve 并不应该平级放置,但在 L2 抽象中并没有办法,但在 L3 中,则完全可以将更容易变化的变量作为返回的过程依赖的参数后续提供,这意味着我们提供了一种像洋葱一样的模型,核心是最不容易变化的部分,而从核心到外围,每一层都生产新的过程,每个过程都依赖更容易变化的变量,这种模型可以很好的应对代码变动、修改对核心功能造成的影响,以保证核心代码的可靠性,是一种开发的最佳实践。